Recursive Algorithm

Recursive Algorithm

As recursion is the process of defining a problem/solution in terms of a simpler version of itself, a recursive algorithm is an algorithm that calls itself with simpler parameters.

Recursion comes directly from Mathematics, where there are many examples of expressions written in terms of themselves. A well-known example is the Fibonacci sequence as defined:

F(i) = F(i-1) + F(i-2)

Before we start, we need to learn about the 3 laws of recursion. These 3 laws apply to all recursive algorithms, without any of the 3 laws it is not considered a recursive algorithm.

1. Must have a base case (aka terminating condition)
2. Must change its state and move towards the base case
3. Must call itself recursively

Let’s use the Fibonacci sequence example and write a recursive algorithm.

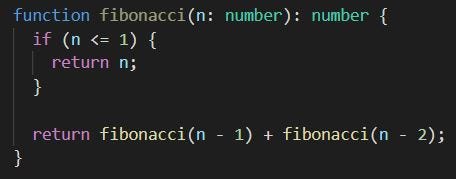
Code snippet of fibonacci function in Typescript

The code snippet was written in Typescript. It is a function that takes a number as an input, and outputs a number.

As mentioned, the 3 laws of recursion applies to this function.

1. Must have a base case; if (n ≤ 1)
2. Must change its state and move towards base case; return fibonacci(n-1) + fibonacci(n-2);
3. Must call itself recursively; return fibonacci(n-1) + fibonacci(n-2);

Given the algorithm above, let’s see if we can figure out what F(5) equates to. I’ve created a diagram to help you visualize and work on it.

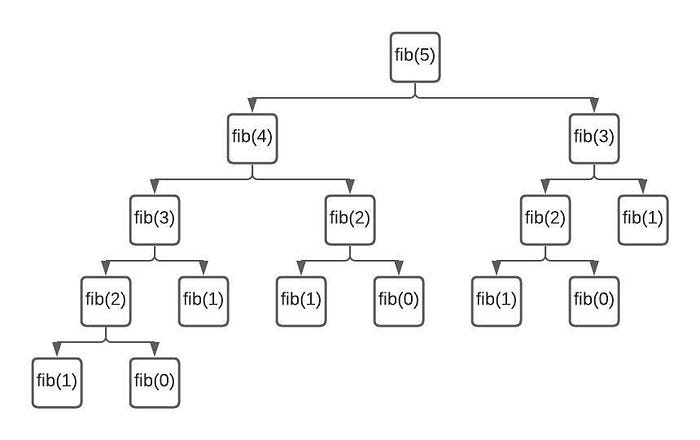
If you were able to work it out, you should arrive at the answer 5.

If not, here are the steps.

• Remember the terminating condition if(n ≤ 1) it returns n, which is also the input. So all fib(0) and fib(1) will give you 1.
• Anything above 1 is simply the sum of one level down, i.e. fib(2) = fib(1) + fib(0)

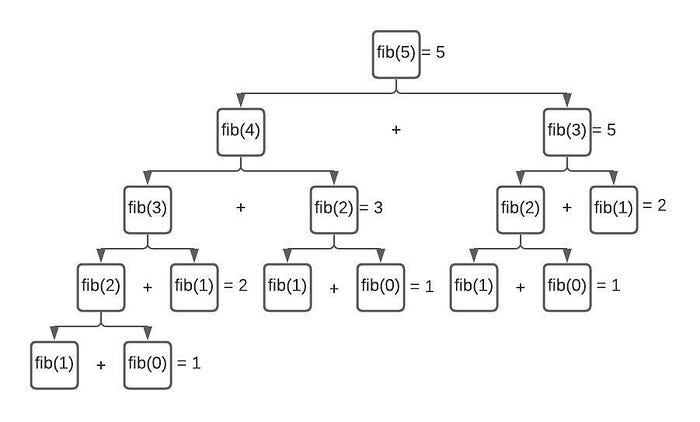
If you’d like to try out some other inputs, here’s a cheat sheet for you to check your answer against.

Do note that all recursive functions can be converted to iterative functions and vice versa. So why use recursive functions instead of iterative functions? We’ll talk about that in the next post.